Алгоритмы сортировки

Сортировка пузырьком (Bubble sort)

Сортировка пузырьком - это базовый алгоритм сортировки, который последовательно сравнивает и меняет местами пары соседних элементов, если они находятся в неправильном порядке.

Алгоритм

Алгоритм сортировки пузырьком работает следующим образом:

Проходим по массиву, сравнивая попарно соседние элементы.
Если элементы находятся в неправильном порядке, меняем их местами.
Повторяем процесс до тех пор, пока весь массив не будет отсортирован.

Анализ сложности

Временная сложность сортировки пузырьком: В худшем и лучшем случаях $O (n^{2})$ , где $n$ - количество элементов.
Пространственная сложность сортировки пузырьком: $O (1)$ , так как сортировка происходит "на месте" без использования дополнительных структур данных.

Реализация

Приведём примеры реализации сортировки пузырьком:

PythonC++Java

Python

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
    return arr

C++

#include <vector>

void bubbleSort(std::vector<int>& arr) {
    int n = arr.size();
    for (int i = 0; i < n-1; i++) {
        for (int j = 0; j < n-i-1; j++) {
            if (arr[j] > arr[j+1]) {
                std::swap(arr[j], arr[j+1]);
            }
        }
    }
}

Java

public void bubbleSort(int[] arr) {
    int n = arr.length;
    for (int i = 0; i < n-1; i++) {
        for (int j = 0; j < n-i-1; j++) {
            if (arr[j] > arr[j+1]) {
                int temp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = temp;
            }
        }
    }
}

Заключение

Сортировка пузырьком, хотя и является одним из самых простых алгоритмов сортировки, играет важную роль в обучении основам алгоритмических техник. Её простота делает её отличным выбором для понимания базовых принципов сортировки и алгоритмического мышления.

Несмотря на свою неэффективность в сравнении с более продвинутыми алгоритмами сортировки, такими как быстрая сортировка или сортировка слиянием, сортировка пузырьком находит своё применение в образовательных целях и в ситуациях, где простота реализации является ключевым фактором. Она также может быть эффективной на небольших или частично отсортированных массивах данных.

Сортировка вставками (Insertion sort)

Сортировка вставками - это простой алгоритм сортировки, который строит отсортированный массив (или список), вставляя каждый новый элемент в уже отсортированную последовательность.

Алгоритм

Алгоритм сортировки вставками работает следующим образом:

Начинаем с первого элемента массива, считая его уже отсортированным.
Берем следующий элемент и сравниваем его с элементами в отсортированной части массива.
Вставляем этот элемент в правильное место в отсортированной части.
Повторяем процесс для всех элементов.

Анализ сложности

Временная сложность сортировки вставками: В худшем случае $O (n^{2})$ , где $n$ - количество элементов. В лучшем случае - $O (n)$ , если массив уже отсортирован.
Пространственная сложность сортировки вставками: $O (1)$ , так как сортировка происходит "на месте" без использования дополнительных структур данных.

Реализация

Приведём примеры реализации сортировки вставками:

PythonC++Java

Python

def insertion_sort(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i - 1
        while j >= 0 and key < arr[j]:
            arr[j + 1] = arr[j]
            j -= 1
        arr[j + 1] = key
    return arr

C++

#include <vector>

void insertionSort(std::vector<int>& arr) {
    int n = arr.size();
    for (int i = 1; i < n; i++) {
        int key = arr[i];
        int j = i - 1;

        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j = j - 1;
        }
        arr[j + 1] = key;
    }
}

Java

public void insertionSort(int arr[]) {
    int n = arr.length;
    for (int i = 1; i < n; ++i) {
        int key = arr[i];
        int j = i - 1;

        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j = j - 1;
        }
        arr[j + 1] = key;
    }
}

Заключение

Сортировка вставками является одним из фундаментальных алгоритмов в области компьютерных наук, особенно ценным для понимания базовых принципов алгоритмической эффективности и техник сортировки. Хотя она может быть не такой быстрой, как некоторые более сложные алгоритмы сортировки, её простота и эффективность на небольших или почти отсортированных наборах данных делают её полезной во многих практических ситуациях.

Этот алгоритм особенно полезен в сценариях, где данные поступают последовательно и должны быть отсортированы сразу при получении. Его простота также делает его отличным выбором для начинающих программистов, стремящихся улучшить свои навыки в написании эффективного и понятного кода.

Сортировка слиянием (Merge sort)

Сортировка слиянием - это эффективный алгоритм сортировки, использующий подход "разделяй и властвуй". Он разбивает массив на две половины, рекурсивно сортирует их, а затем объединяет отсортированные половины.

Алгоритм

Алгоритм сортировки слиянием работает следующим образом:

Разделить массив на две половины.
Рекурсивно сортировать каждую половину.
Объединить две отсортированные половины в один отсортированный массив.

Анализ сложности

Временная сложность сортировки слиянием: Во всех случаях $O (n \log n)$ , где $n$ - количество элементов.
Пространственная сложность сортировки слиянием: $O (n)$ , так как требуется дополнительное пространство для временного хранения подмассивов.

Реализация

Приведём примеры реализации сортировки слиянием:

PythonC++Java

Python

def merge_sort(arr):
    if len(arr) > 1:
        mid = len(arr) // 2
        L = arr[:mid]
        R = arr[mid:]

        merge_sort(L)
        merge_sort(R)

        i = j = k = 0

        while i < len(L) and j < len(R):
            if L[i] < R[j]:
                arr[k] = L[i]
                i += 1
            else:
                arr[k] = R[j]
                j += 1
            k += 1

        while i < len(L):
            arr[k] = L[i]
            i += 1
            k += 1

        while j < len(R):
            arr[k] = R[j]
            j += 1
            k += 1

C++

#include <vector>

void merge(std::vector<int>& arr, int const left, int const mid, int const right) {
    auto const subArrayOne = mid - left + 1;
    auto const subArrayTwo = right - mid;

    std::vector<int> leftArray(subArrayOne), rightArray(subArrayTwo);

    for (auto i = 0; i < subArrayOne; i++)
        leftArray[i] = arr[left + i];
    for (auto j = 0; j < subArrayTwo; j++)
        rightArray[j] = arr[mid + 1 + j];

    auto indexOfSubArrayOne = 0, indexOfSubArrayTwo = 0;
    int indexOfMergedArray = left;

    while (indexOfSubArrayOne < subArrayOne && indexOfSubArrayTwo < subArrayTwo) {
        if (leftArray[indexOfSubArrayOne] <= rightArray[indexOfSubArrayTwo]) {
            arr[indexOfMergedArray] = leftArray[indexOfSubArrayOne];
            indexOfSubArrayOne++;
        } else {
            arr[indexOfMergedArray] = rightArray[indexOfSubArrayTwo];
            indexOfSubArrayTwo++;
        }
        indexOfMergedArray++;
    }
    while (indexOfSubArrayOne < subArrayOne) {
        arr[indexOfMergedArray] = leftArray[indexOfSubArrayOne];
        indexOfSubArrayOne++;
        indexOfMergedArray++;
    }
    while (indexOfSubArrayTwo < subArrayTwo) {
        arr[indexOfMergedArray] = rightArray[indexOfSubArrayTwo];
        indexOfSubArrayTwo++;
        indexOfMergedArray++;
    }
}

void mergeSort(std::vector<int>& arr, int const begin, int const end) {
    if (begin >= end)
        return;

    auto mid = begin + (end - begin) / 2;
    mergeSort(arr, begin, mid);
    mergeSort(arr, mid + 1, end);
    merge(arr, begin, mid, end);
}

Java

public void mergeSort(int[] arr, int l, int r) {
    if (l < r) {
        int m = l + (r - l) / 2;

        mergeSort(arr, l, m);
        mergeSort(arr, m + 1, r);

        merge(arr, l, m, r);
    }
}

private void merge(int[] arr, int l, int m, int r) {
    int n1 = m - l + 1;
    int n2 = r - m;

    int[] L = new int[n1];
    int[] R = new int[n2];

    for (int i = 0; i < n1; ++i)
        L[i] = arr[l + i];
    for (int j = 0; j < n2; ++j)
        R[j] = arr[m + 1 + j];

    int i = 0, j = 0;

    int k = l;
    while (i < n1 && j < n2) {
        if (L[i] <= R[j]) {
            arr[k] = L[i];
            i++;
        } else {
            arr[k] = R[j];
            j++;
        }
        k++;
    }

    while (i < n1) {
        arr[k] = L[i];
        i++;
        k++;
    }

    while (j < n2) {
        arr[k] = R[j];
        j++;
        k++;
    }
}

Заключение

Сортировка слиянием представляет собой мощный и эффективный алгоритм, который является отличным примером применения стратегии "разделяй и властвуй" в алгоритмических задачах. Благодаря своей способности эффективно обрабатывать большие объемы данных, сортировка слиянием часто используется в реальных приложениях, где необходима высокая производительность сортировки.

Одним из ключевых преимуществ сортировки слиянием является её стабильность и предсказуемость производительности, что делает её предпочтительным выбором в ситуациях, где важна гарантия времени выполнения. Однако, необходимость в дополнительном пространстве для хранения подмассивов может быть ограничивающим фактором в средах с ограниченными ресурсами памяти.

Быстрая сортировка (Quick sort)

Быстрая сортировка - это эффективный алгоритм сортировки, использующий стратегию "разделяй и властвуй". Он выбирает один элемент в качестве опорного и разделяет массив на две части: элементы меньше опорного и элементы больше опорного, затем рекурсивно применяет ту же стратегию к этим подмассивам.

Алгоритм

Алгоритм быстрой сортировки работает следующим образом:

Выбираем опорный элемент из массива.
Перегруппировываем элементы в массиве так, что элементы меньше опорного перемещаются перед ним, а большие - после.
Рекурсивно применяем те же шаги к подмассивам слева и справа от опорного элемента.

Анализ сложности

Временная сложность быстрой сортировки: В среднем и худшем случаях $O (n \log n)$ , где $n$ - количество элементов. В худшем случае (когда каждый раз выбирается наихудший опорный элемент) - $O (n^{2})$ .
Пространственная сложность быстрой сортировки: $O (\log n)$ из-за использования стека вызовов при рекурсии.

Реализация

Приведём примеры реализации быстрой сортировки:

PythonC++Java

Python

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quick_sort(left) + middle + quick_sort(right)

C++

#include <vector>

void quickSort(std::vector<int>& arr, int low, int high) {
    if (low < high) {
        int pivot = partition(arr, low, high);
        quickSort(arr, low, pivot - 1);
        quickSort(arr, pivot + 1, high);
    }
}

int partition(std::vector<int>& arr, int low, int high) {
    int pivot = arr[high];
    int i = (low - 1);

    for (int j = low; j <= high - 1; j++) {
        if (arr[j] < pivot) {
            i++;
            std::swap(arr[i], arr[j]);
        }
    }
    std::swap(arr[i + 1], arr[high]);
    return (i + 1);
}

Java

public void quickSort(int[] arr, int low, int high) {
    if (low < high) {
        int pi = partition(arr, low, high);
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}

private int partition(int[] arr, int low, int high) {
    int pivot = arr[high]; 
    int i = (low - 1);
    for (int j = low; j < high; j++) {
        if (arr[j] < pivot) {
            i++;
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
    }
    int temp = arr[i + 1];
    arr[i + 1] = arr[high];
    arr[high] = temp;
    return i + 1;
}

Заключение

Быстрая сортировка, известная своей высокой эффективностью и широким применением, является одним из ключевых алгоритмов в области компьютерных наук. Её способность быстро обрабатывать большие объемы данных делает её предпочтительным выбором для многих приложений, требующих эффективной сортировки.

Основываясь на стратегии "разделяй и властвуй", быстрая сортировка обеспечивает хорошую производительность в среднем и лучшем случаях, хотя в худшем случае её производительность может снижаться до . Это делает важным выбор опорного элемента и может потребовать дополнительных оптимизаций в зависимости от характера входных данных.

Сортировка Шелла (Shell sort)

Сортировка Шелла - это усовершенствованная версия сортировки вставками, которая позволяет уменьшить количество сравнений и перемещений элементов за счет использования промежуточных шагов.

Алгоритм

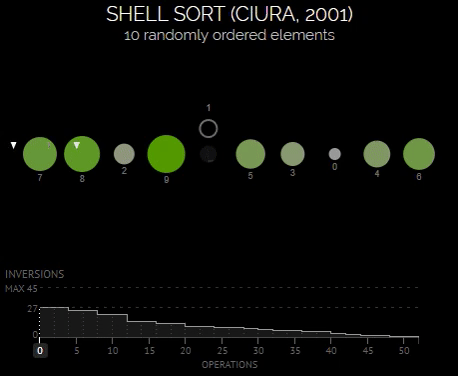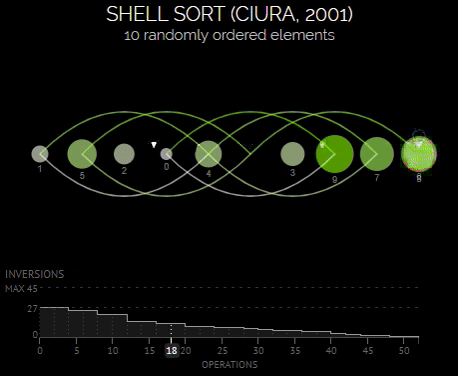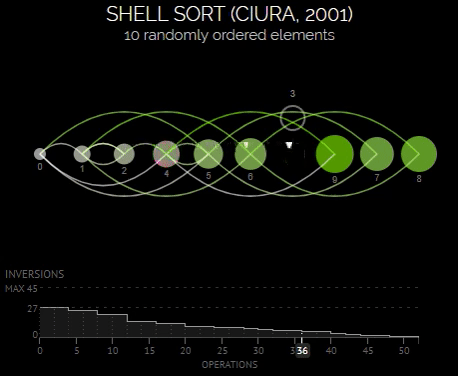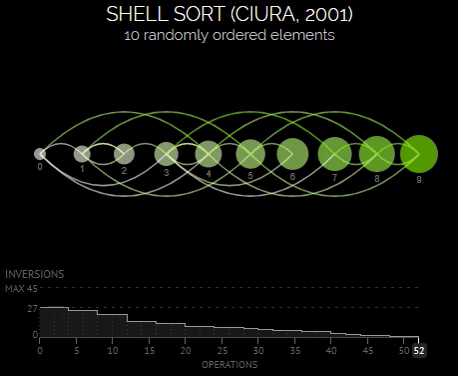
Алгоритм сортировки Шелла работает следующим образом:

Выбор начального значения шага, обычно равного половине длины массива.
Выполнение сортировки вставками для элементов, находящихся на расстоянии шага друг от друга.
Постепенное уменьшение шага и повторение процесса, пока шаг не станет равным 1.
На последнем шаге алгоритм выполняется как обычная сортировка вставками.

Анализ сложности

Временная сложность сортировки Шелла: Зависит от выбора шагов. В худшем случае может достигать $O (n^{2})$ , но обычно работает значительно быстрее.
Пространственная сложность сортировки Шелла: $O (1)$ , так как сортировка выполняется на месте.

Реализация

Приведём примеры реализации сортировки Шелла:

PythonC++Java

Python

def shell_sort(arr):
    n = len(arr)
    gap = n // 2

    while gap > 0:
        for i in range(gap, n):
            temp = arr[i]
            j = i
            while j >= gap and arr[j - gap] > temp:
                arr[j] = arr[j - gap]
                j -= gap
            arr[j] = temp
        gap //= 2
    return arr

C++

#include <vector>

void shellSort(std::vector<int>& arr) {
    int n = arr.size();
    for (int gap = n / 2; gap > 0; gap /= 2) {
        for (int i = gap; i < n; i += 1) {
            int temp = arr[i];
            int j;
            for (j = i; j >= gap && arr[j - gap] > temp; j -= gap)
                arr[j] = arr[j - gap];
            arr[j] = temp;
        }
    }
}

Java

public void shellSort(int[] arr) {
    int n = arr.length;

    for (int gap = n / 2; gap > 0; gap /= 2) {
        for (int i = gap; i < n; i++) {
            int temp = arr[i];
            int j;
            for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {
                arr[j] = arr[j - gap];
            }
            arr[j] = temp;
        }
    }
}

Заключение

Сортировка Шелла является более эффективной альтернативой традиционной сортировке вставками, особенно для больших массивов, благодаря использованию шагов, которые позволяют элементам быстрее достигать своего конечного положения в отсортированном массиве.

Алгоритмы сортировки ​

Сортировка пузырьком (Bubble sort) ​

Алгоритм ​

Анализ сложности ​

Реализация ​

Заключение ​

Сортировка вставками (Insertion sort) ​

Алгоритм ​

Анализ сложности ​

Реализация ​

Заключение ​

Сортировка слиянием (Merge sort) ​

Алгоритм ​

Анализ сложности ​

Реализация ​

Заключение ​

Быстрая сортировка (Quick sort) ​

Алгоритм ​

Анализ сложности ​

Реализация ​

Заключение ​

Сортировка Шелла (Shell sort) ​

Алгоритм ​

Анализ сложности ​

Реализация ​

Заключение ​

Алгоритмы сортировки

Сортировка пузырьком (Bubble sort)

Алгоритм

Анализ сложности

Реализация

Заключение

Сортировка вставками (Insertion sort)

Алгоритм

Анализ сложности

Реализация

Заключение

Сортировка слиянием (Merge sort)

Алгоритм

Анализ сложности

Реализация

Заключение

Быстрая сортировка (Quick sort)

Алгоритм

Анализ сложности

Реализация

Заключение

Сортировка Шелла (Shell sort)

Алгоритм

Анализ сложности

Реализация

Заключение